A cute, real life probability problem

You log in to discord and you see all of your friends are in there chatting. Excited, you join and ask “5 q?”, soon thereafter you’re all in a CS:GO lobby ready to play. You’re done with your homework (or normal work now that I’m an adult), everything is perfect, what could go wrong? Then you see the wait times:

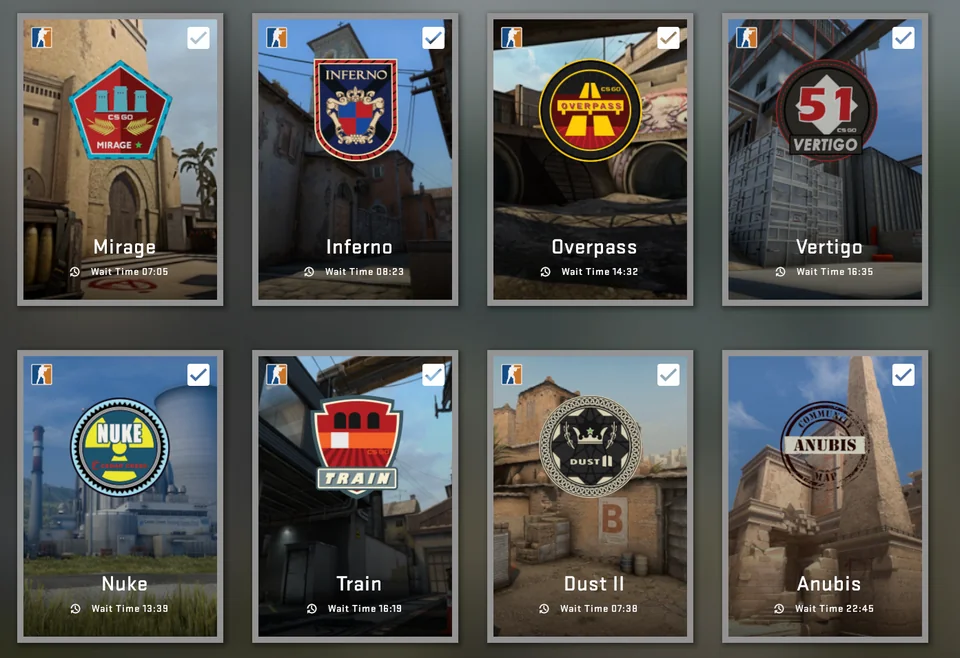
Damn it… looks like we’ll be in the queue for a bit, let’s try adding more maps since it will decrease our overall expected wait time you say, intuitively…

This makes a lot of sense, but I noticed it wasn’t immediately clear to me by how much my wait time would decrease, so I thought about it some more…

Modeling the problem

I decided to start by modelling the wait time for each map as a normally distributed random variable, where the mean equals the expected wait time, in other words: $\mu = E[X]$. This is probably not actually the case, I’m thinking it’s heavily left skewed, i.e. its much more likely you will wait 10 seconds than 20 minutes, but this will do for now.

When we are only queuing one map $X$ our expected wait time is simply $E[X]$, but what if we are also queuing map $Y$, then our expected wait time is $E[\min X,Y]$, that is we will only wait as long as the earliest map we find a game for. But what is this value?

The solution

It turns out the answer to this is not very simple at all, in fact there doesn’t appear to exist a general closed form solution for $n$ normally distributed random variables, although our friend Alex from that post does tell us that this is a “cute” problem because a closed form solution exists for $n\in {1,2,3,4,5}$. He says, for $n=2$ and $X, Y \sim N(\mu, \sigma^2)$ then $E[\min X,Y] = \mu - \sigma \pi^{-1/2}$ — woah! did not expect to see $\pi$ in this blog post. You can look at the linked stack exchange answer to see how he derives these (it’s not at all trivial, there are many confusing steps involving integration tricks).

So, let’s say we have a mean of 10 and standard deviation of 2 minutes for both maps, our expected wait time is: $10 - 2\pi^{-1/2} \approx 8.87$ minutes — I confirmed this by computing it in code! Of course this still seems like a long time so I think I would want to queue up to 5 maps. In that case (from that same post) our expected wait time would be $E[\min X_1..X_5] = \mu - \sigma E_5$ where $E_5=\frac{5}{2}\pi^{-3/2}\cos^{-1}(-23/27)$, thus we will most likely wait $10-2[\frac{5}{2}\pi^{-3/2}\arccos(-23/27)]\approx7.67$ minutes.

Conclusion

You’ll notice the diminishing marginal returns here: queuing one more map saves us $1.2$ minutes, but queuing four more maps after that only saves us the same amount of time: $1.2$ minutes. What does this mean for us? Next time we want to save some time, it’s okay to add a few more maps — but for the love of god, we don’t have to add Nuke.