UniV3 pricing functions & optimal arbitrage

In one of my previous blog posts I went over how one can calculate the optimal amount to trade between two constant product liquidity pools of the same assets that have become imbalanced, in order to maximize profit in $O(1)$ time — one need not calculate this with a closed form solution, in fact the winningest ethereum MEV bot of 2021 used a sort of binary search to find it, I just thought it would be cool to derive since it is possible. However, this methodology doesn’t quite work with new pricing functions that aim to reduce the price impact of swaps by concentrating liquidity across certain price ranges. The UniV3 whitepaper offers this figure which helps to understand how the new mechanism (3) differs from a traditional constant product pool (1):

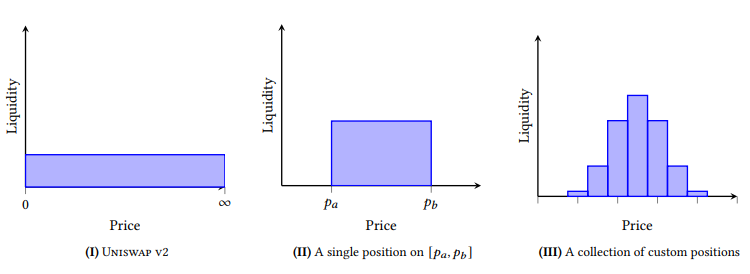
In short, there is much greater liquidity across the price in which you are most likely to trade at, hence the price impact of your swaps (assuming your swap is not big enough such that is crosses into a lot of higher tick ranges) is much smaller. This also increases the capital efficiency of liquidity providers which in turn yields higher returns, so it really seems like a win win.

New pricing mechanism implications

With this new mechanism of pricing the constant product invariant is only maintained accross a given price (or tick) range. Meaning that once the price of the marginal token is above the maximum of this range, we enter a new pricing function on the rest of our amount to be traded — the one that corresponds to the next tick range. I believe that the total liquidity provided within a single tick — and thus the constants that are used to calculate the pricing function within that specific tick — is the sum of liquidity of all the positions that include that tick in their tick range boundaries. However, this is actually not very well documented, even the whitepaper itself doesn’t address this very explicitly, saying merely:

Each tick tracks $\Delta L$, the total amount of liquidity that should be kicked in or out when the tick boundary is crossed.

Where $L = \sqrt{xy}$ and $x, y$ are the amounts of token2 and token1 respectively.

Clearly if we have two pools of the same tokens, and they are trading at different rates, we can buy one at a discount in the cheaper pool and then sell it at a premium on the other. However, in this case there is not a closed form solution for the optimal amount to trade since the constant product assumption only holds within one tick, after we cross into the next boundary we will have to use the new price and liquidity amounts for that tick. So, sadly we can no longer do this calculus in $O(1)$ time… or can we?!

A different approach

Here I simulate 2 UniV3 pools that trade $X/Y$, one for 3.99, and the other for 4.00. I provided liquidity for both pools at each tick according to a normal distribution where the mean is the current price and hence the tick we are currently trading at. I believe this is the optimal distribution of liquidity but I haven’t thought very deeply about it, however the UniV3 paper seems to agree — at least the diagram I showed earlier seems to. In this case I simulate the trade of some amount $x$ going from $Y \rightarrow X \rightarrow Y$, where I buy $X$ on the cheaper pool and sell it on the more expensive one.

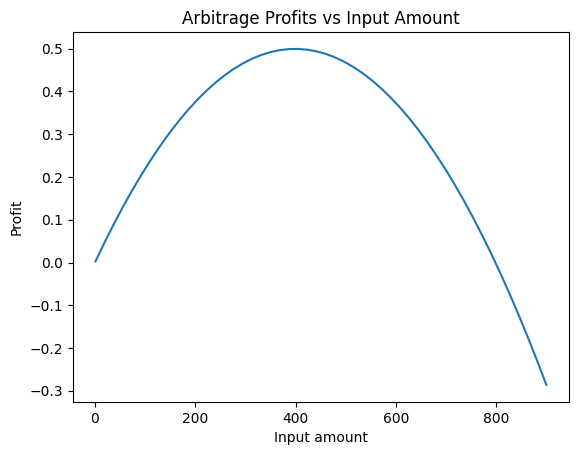
This looks exactly like a parabola to me, and you might think that this is because it is trading within a single tick, but this is not the case. In fact, we cross into a higher tick range for $x > 637.50$. So how do we find the peak of this parabola? Well, we know that $n+1$ points uniquely define a polynomial of degree $n$, so we can take 3 samples of our input amounts vs. arbitrage profits and find this function $ax^2+bx+c$, then we simply $\frac{d}{dx}[ax^2+bx+c]=0 \rightarrow x^* = \frac{-b}{2a}$.

Let’s see if that makes sense by putting our own example to the test:

1. First we take 3 points and see what their profits are, I will take 200, 201, 202 i.e. $f(200) \approx 0.3755, f(201)\approx 0.3767, f(202)\approx 0.3779$
2. Second, we will solve this system of equations. I will do it using matrices because I feel inspired after watching Gil Strangs last linear algebra lecture:

Finally, we calculate our optimal amount based off these coefficients: $x^* = \frac{-0.0025}{2\cdot-3.14\times10^{-6}} = 398.01$ for a maximum profit of $0.498$.

This answer corresponds to the maximum we see in our graph, and we found it in $O(1)$ time 👌

My UniV3 code

import logging

class Position():
  liquidity = 0
  lower_tick = None
  upper_tick = None

  def __init__(self, lower_tick, upper_tick, liquidity):
    self.liquidity = liquidity
    self.lower_tick = lower_tick
    self.upper_tick = upper_tick

class Pool():
  def __init__(self, price_of_token1):
    self.positions = []
    self.sqrt_price = price_of_token1 ** (1/2)
    self.ticks = [self.sqrt_price * 1.001 ** (i/2) for i in range(-1_000, 1_001, 2)]
    self.logger = logging.getLogger()

  def get_current_liquidity(self):
    L = 0
    for position in self.positions:
      if position.lower_tick <= self.sqrt_price < position.upper_tick:
        L += position.liquidity

    return L

  def get_current_tick(self):
    for i, tick in enumerate(self.ticks):
      if i == len(self.ticks) - 1:
        return i

      if tick <= self.sqrt_price < self.ticks[i+1]:
        return i

  def calculate_swap(self, amount_in, token_in):
    if amount_in <= 0.0001:
      return 0

    L = self.get_current_liquidity()
    if token_in == "token1":
      max_sqrt_price = self.ticks[self.get_current_tick() + 1]
      max_sqrt_price_diff = max_sqrt_price - self.sqrt_price
      max_amount_in_for_tick = max_sqrt_price_diff * L

      current_exchange = min(amount_in, max_amount_in_for_tick)
      new_sqrt_price = current_exchange / L + self.sqrt_price

      inverse_sqrt_price_delta = (1 / new_sqrt_price - 1 / self.sqrt_price)
      amount_out = -1 * inverse_sqrt_price_delta * L

      self.logger.debug("TOKEN1 -> TOKEN2 SWAP LOG: %s",
       {
          "amount_in": amount_in,
          "L": L,
          "max_sqrt_price": max_sqrt_price,
          "max_sqrt_price_diff": max_sqrt_price_diff,
          "max_amount_in_for_tick": max_amount_in_for_tick,
          "new_sqrt_price": new_sqrt_price,
          "inverse_sqrt_price_delta": inverse_sqrt_price_delta,
          "amount_out": amount_out
        }
      )

      # Set the new price and return amount out + potentially calculate rest of
      # amount out at new price if we didn't finish
      self.sqrt_price = new_sqrt_price
      return amount_out + self.calculate_swap(amount_in - current_exchange, token_in)
    else:  # token_in == "token2"
      min_sqrt_price = self.ticks[self.get_current_tick() - 1]
      max_inverse_sqrt_price_diff = abs(1 / self.sqrt_price - 1 / min_sqrt_price)
      max_amount_in_for_tick = max_inverse_sqrt_price_diff * L

      current_exchange = min(amount_in, max_amount_in_for_tick)
      new_sqrt_price = self.sqrt_price * L / (current_exchange * self.sqrt_price + L)

      sqrt_price_delta = self.sqrt_price - new_sqrt_price
      amount_out = sqrt_price_delta * L

      self.logger.debug("TOKEN2 -> TOKEN1 SWAP LOG: %s",
       {
          "amount_in": amount_in,
          "L": L,
          "min_sqrt_price": min_sqrt_price,
          "max_inverse_sqrt_price_diff": max_inverse_sqrt_price_diff,
          "max_amount_in_for_tick": max_amount_in_for_tick,
          "new_sqrt_price": new_sqrt_price,
          "sqrt_price_delta": sqrt_price_delta,
          "amount_out": amount_out
        }
      )

      # Set the new price and return amount out + potentially calculate rest of
      # amount out at new price if we didn't finish
      self.sqrt_price = new_sqrt_price
      return amount_out + self.calculate_swap(amount_in - current_exchange, token_in)

  def add_position(self, lower_tick, upper_tick, liquidity):
    self.positions.append(Position(lower_tick, upper_tick, liquidity))